男のロマン詰め放題!知って得する方程式
みなさん、こんにちは。初記事を書かせていただきます。1男のChamp です。
夏休みも佳境にさしかかりもうすぐ成績発表ということでドキドキワクワクヒヤヒヤしていることでしょう。
個人の感想としては、夏休みは暇を持て余してしまい、学校が始まることをうれしく思っています。
しかし、そうはいってもやはり勉強はつらい。
好きなこと勉強するのはいいけどなんで文系大学来てまで数学の授業受けなきゃいけないんだ……なんて思っている生徒も少なくないですよね。
そこで、突然ですが問題です。
以下の方程式を解いてください。
4X+7Y=13
5X-2Y=-16
もちろん正解は、
X=-2 Y=3
文系大学とはいえ、国公立文系最高峰を 自称 する一橋生ならお茶の子さいさいですよね?
ここでは間違った~という反応は期待していません。。。。。
けど、こんなことを考えたりしたことはありませんか?
実社会で方程式使うことなんてあるはずない。だから、自分は数学苦手でも全然困らない。
確かに私立文系が活躍しているのですから、困らないのかもしれませんね。
しかし!!!
せっかく今まで勉強してきたんだからちょっとは数学を使った雑学でちやほやされてもいいはずですよね?
いや、ちやほやしてください!!
ということで、今回は知って得する雑学方程式を紹介します。
誕生日を当てる方程式

合コンとかに行くと誕生日を聞いたりしますよね!(筆者は行ったことがありません泣)
女性は誕生日の話が好きです。(偏見)
そこで、誕生日いつ?と単純に聞くだけでは芸がありません。
せっかくなら少し凝ったことをしようではありませんか!
1) 生まれた月に「2」をかける
2) その答えに「5」を足す
3) その答えに「50」をかける
4) その答えに生まれた日を足す
5) その答えから「250」を引く
例えば10月7日生まれの人の場合は……
1)10×2=20
2) 20+5=25
3) 25×50=1250
4) 1250+7=1257
5) 1257-250=1007
1007→10月7日
当たりましたね!!
これを使って合コンを楽しみましょう!!!
宇宙人の数を求める方程式
みなさんの中には夏休みに東京を離れて空気のきれいな高原で夜空に星を眺めに行くなんていうロマンチストもいるのではないでしょうか??
心なしか一橋にはそういう人が多い気がします。

さて、宇宙人、特に火星人を想像しろって言われると
タコみたいな姿を想像しませんか??
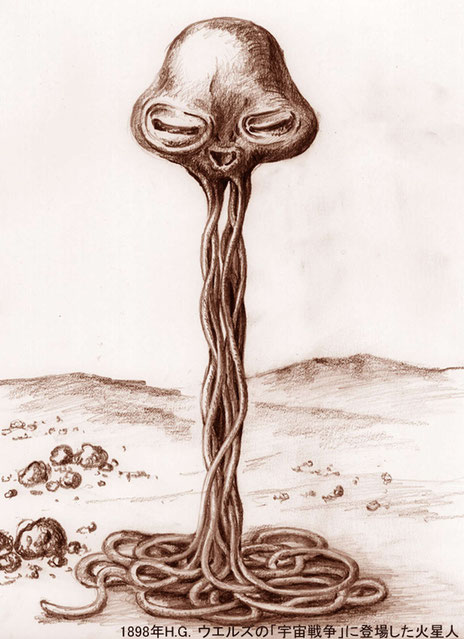
火星は地球より重力が弱いから手足の筋肉が発達せず貧弱で細いだろう、文明は地球より優れているから脳が発達していて頭がデカイはずだ、という考えからタコもどきのイメージが浸透したようです。
地球という惑星にこうやって生命が存在する以上、宇宙の地球と同じ様な条件の惑星には必然的に生命が存在しているはずですよね。
宇宙には"天文学的な"数の星がありますから、宇宙人も様々なんでしょう。
単細胞生物みたいな単純なもの、我々みたいにある程度の知能を持っているもの、あるいはもーっと高度な文明を持つもの……。
さて、宇宙に関する方程式の一つに『ドレイクの方程式』というものがあります。
これは、1961年にアメリカの天文学者フランク・ドレイクさんが提唱した、この宇宙にどれくらいの星間通信可能な知的生命体が存在するかを推定する為の式です。
これで宇宙人は存在するのかという永遠の疑問を解消できるのです!!
N=R*×fp×ne×fl×fi×fc×L
N=星間通信を行うような高度な文明を持つ生命体の数
R*=我々の銀河系で恒星が形成される速度
fp=惑星を有する恒星の割合
ne=ひとつの恒星系で生命体が発生可能となる惑星の平均数
fl=その惑星で生命が発生する割合
fi=その生命体が知的生命体にまで進化する割合
fc=その生命体が星間通信を行う割合
L=文明の推定存続期間
うーん、なんかよくわからないですね。ちょっと文系の僕たちの想像を絶するような世界なのかもしれません。けど、人間以外にも高度な文明を有する生命体が存在するということですね。
いやーなかなかロマンに溢れてます!
パンチラ成功の方程式
では、最後に男子必見の方程式を紹介しましょう。(女子は心穏やかにそっと読み進めてください。)
これもドレイクの方程式並みにロマンが詰まっていますよ!!
男子のみなさん、一度はパンチラを試みたことはないでしょうか??

共学だったら学校の階段、男子校なら駅の階段やエスカレータなどなど日常生活に結構チャンスは転がっているものですよね。
しかし、なかなか成功することは少ない、というかギリギリ見えないからこそいい!!
みたいな意見もよく男子だけで集まったりすると耳にします。
そんなパンチラ、なんと見えるかどうかは方程式で解くことができちゃうんです。
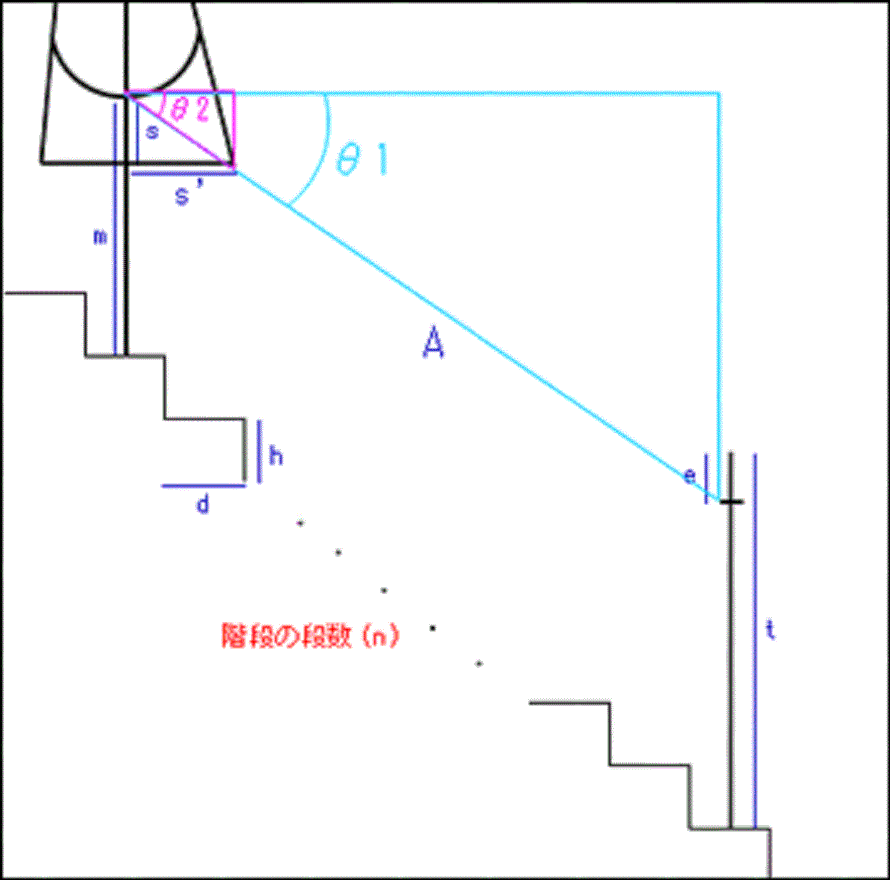
下の図を見てください。
s:スカートの長さ(股から裾まで)
s':スカートの後ろ幅
m:股下の長さ
t:身長
e:目線の位置(頭から目までの長さ)
h:階段の高さ
d:階段の幅
n:階段の段数
パンチラが見えると言う事は、図中のAライン(視線)の延長に パンツ があるということです。
つまり、水色の三角形の角度θ1(シータワン)が、ピンクの三角形の角度θ2(シータツー)を上回れば目的が達成されるのです。
これを式で表すと
tanθ2 < tanθ1
となります。
さらにこの式を各パラメータを用いて書き換えると、
s/s' < (hn+m-(t-e))/dn
となります。(パラメータに、新たにスカートの後ろ幅 s' を追加しました)
この式が成立する時の階段の段数nを求めれば、理論上パンチラが発生するということになるのです。
実際に自分の身長をあてはめてみました!!
スカートの長さ(s):6cm
スカートの後ろ幅(s´):12cm
ターゲットの股下(m):74cm
自分の身長(t):175cm
目線の位置(e):13cm
階段の高さ(h):20cm
階段の幅(d):28cm
としたならば、上記の式(s/s' < (hn+m-(t-e))/dn)に当てはめ、
6/12 < (20n+74-(175-13))/28n
44/3<n
よって、15段以上離れていれば成功ということです!!!
少し遠いですね……見えるかな汗
ちなみにこれらの計算は高校一年レベルの数学です!!
まさか文系最高峰の一橋大学に通う生徒で理解できないなんていう生徒はいないでしょうが、もし法学部や社会学部で「数学なんて実社会で役に立たない」などと言って勉強を怠っていた諸君!!
数学は立派に実社会で役に立つ のです!
数学は夢を現実に導いてくれる のです!!
さぁ早く早く青チャートの三角関数のページを開いて復習復習!!!!
いかがでしたか?
いままで数学ガチ勢だったみなさん、「数学やっててよかったー!!」と思えましたか?思いましたよね?
そうでなかったみなさんは、冬学期、ぜひ数学をとりましょう!!!!
この記事をシェアしよう!
あわせて読みたい